La matematica è pazza. Mentre le basi sono piuttosto semplici, la filosofia dietro alcuni di questi fondamentali molto semplici può essere abbastanza profonda ... e persino sconcertante. Oggi guarderemo tutto, dai numeri primi all'infinito. Quindi preparati perché questi sono 25 principi matematici straordinari per sfidare il tuo cervello!
La corda dell'equatore
 Fonte: abc.net.au, Immagine: pexels (dominio pubblico)
Fonte: abc.net.au, Immagine: pexels (dominio pubblico) Se avessi avvolto una corda intorno all'equatore della Terra in modo da abbracciarlo saldamente al terreno, avresti solo bisogno di aggiungere circa 6, 3 metri di corda in modo che l'intero oggetto si posizionasse a 1 metro sopra il livello del terreno (tutto intorno Terra). Questo risultato controintuitivo funziona indipendentemente dalla grandezza della sfera. Il modo più semplice per spiegare questo è ricordare che la circonferenza è uguale al diametro dei tempi pi. Ciò significa che se vuoi far oscillare la corda a 1 metro sopra la Terra, devi solo aumentare il diametro di 2 metri (1 metro su ogni estremità del globo). Pertanto, è necessario aumentare la circonferenza della fune di 2 x pi metri (6, 28318530718 metri).
Ippopotamo di Metaponto
 Fonte: esoterx.com, Immagine: https://commons.wikimedia.org (dominio pubblico)
Fonte: esoterx.com, Immagine: https://commons.wikimedia.org (dominio pubblico) L'uomo che ha dimostrato che esistevano numeri irrazionali è stato ucciso per questo. Il suo nome era Ippaso di Metaponto e avvenne verso il 520 aC. Pitagora e molti matematici greci dell'epoca ritenevano che tutti i numeri fossero interi o interi. Era quando Pitagora eseguiva i suoi famosi calcoli a triangolo (teorema di Pitagora) che inciampò nella radice quadrata di due. Per farla breve, presumibilmente cercò di mantenere segreto il suo ritrovamento e lo capovolse quando Hippasus lo pubblicò.
Numeri di Munchausen
 Fonte: zach.se
Fonte: zach.se Oltre a fare alcune ipotesi su 0 ^ 0, 3435 è l'unico numero oltre a 1 in cui è possibile dividere ogni cifra, aumentarla alla sua stessa potenza, sommare tutto insieme e ottenere lo stesso numero indietro. Fondamentalmente, 3 ^ 3 + 4 ^ 4 + 3 ^ 3 + 5 ^ 5 = 3435 Nota: 438579088 funziona anche se si assume che 0 ^ 0 = 0. Questi sono chiamati numeri di Munchausen.
La rappresentazione decimale del 7 °
 Immagine: https://pixabay.com (dominio pubblico)
Immagine: https://pixabay.com (dominio pubblico) Le rappresentazioni decimali del 7 sono le stesse serie di numeri che si ripetono eccetto sempre che partono da un punto diverso. 1/7 = 0, 142857142857 ... e 2/7 = 0, 285714285714 ... e 3/7 = 0, 428571428571 ...
Conteggio delle dita binarie
 Fonte: mathisfun.com, immagine: https://pixabay.com (dominio pubblico)
Fonte: mathisfun.com, immagine: https://pixabay.com (dominio pubblico) Se usi il binario, puoi contare fino a 1023 sulle dita.
10!
 Fonte: reddit.com
Fonte: reddit.com Ce ne sono esattamente 10! secondi in 6 settimane. È più facile vederlo quando lo si analizza in questo modo: 6 * 7 * 24 * 60 * 60 = 6 * 7 * (8 * 3) * (3 * 2 * 10) * (1 * 3 * 4 * 5) = 6 * 7 * 8 * 9 * 2 * 10 * 1 * 3 * 4 * 5 = 10!
Il numero di Graham
 Fonte: ibmathresources.com, immagine: https://pixabay.com (dominio pubblico)
Fonte: ibmathresources.com, immagine: https://pixabay.com (dominio pubblico) Il numero di Graham è così grande che se scrivessi ogni cifra il più piccolo possibile, occuperebbe ancora più spazio di quello disponibile nell'universo osservabile. Infatti, se potessi contenere tutte le cifre nella tua testa, il tuo cervello collasserebbe in un buco nero (a causa della densità astronomica delle connessioni neurali di cui avresti bisogno).
Ripetendo i decimali
 Immagine: https://pixabay.com (dominio pubblico)
Immagine: https://pixabay.com (dominio pubblico) Qualsiasi decimale ricorrente può essere scritto come una frazione su un numero equivalente di 9 (come la parte ripetitiva). Ad esempio, .456456456 ... sarebbe 456/999
Mischiare le carte
 Fonte: qi.com, immagine: https://www.pexels.com (dominio pubblico)
Fonte: qi.com, immagine: https://www.pexels.com (dominio pubblico) Ogni volta che mischia casualmente un mazzo di 52 carte, le hai quasi certamente disposte in un ordine completamente unico. Ciò che intendiamo con questo è che nell'intera storia dell'umanità nessuno ha mai mischiato un mazzo nello stesso modo. Come? Bene, ci sono 52! modi in cui è possibile ordinare il mazzo (52 * 51 * 50 ...) Questo porta a 8.0658 x 10 ^ 67 possibilità. In confronto, l'universo è solo 1 x 10 ^ 18 secondi. Anche se hai rimescolato un mazzo ogni secondo dal big bang ... cadi miseramente breve.
La bottiglia di Klein
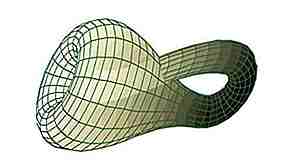 Fonte: math.union.edu
Fonte: math.union.edu Se prendi due strisce di Möbius e ne estendi i bordi in modo che si colleghino (in effetti incollandoli insieme), crei una bottiglia di Klein. Questa "bottiglia" è un esempio di superficie non orientabile. Fondamentalmente, esiste solo in 4 dimensioni, ma può essere liberamente rappresentato in 3. Come la striscia di Möbius, ha solo 1 superficie, ma senza bordi. È piuttosto divertente.
The Frivolous Theorem of Arithmetic
 Fonte: mathworld.wolfram.com, immagine: https://pixabay.com (dominio pubblico)
Fonte: mathworld.wolfram.com, immagine: https://pixabay.com (dominio pubblico) Il teorema frivolo dell'aritmetica afferma che, a causa dell'infinito, la stragrande maggioranza dei numeri naturali è molto, molto grande.
Cosa si trova tra 0 e 1

C'è una quantità infinita di numeri tra 0 e 1 (e 1 e 2, ecc.). Ad esempio, ½, ⅓, ¼, e puoi continuare.
Numeri non calcolabili
 Fonte: igoro.com, immagine: http://www.pixnio.com (dominio pubblico)
Fonte: igoro.com, immagine: http://www.pixnio.com (dominio pubblico) Quasi tutti i numeri reali sono irrazionali. Ancor più, la maggior parte dei numeri irrazionali non è nemmeno calcolabile. E per sconvolgere davvero la tua mente, ogni singolo numero che hai mai visto nella tua vita è computabile, compresi numeri ripetuti all'infinito come pi (perché puoi creare un algoritmo per calcolarlo). Quindi, per semplificare le cose, c'è una quantità infinita di numeri là fuori che non vedremo mai (in realtà ... la maggior parte di essi) perché non abbiamo modo di calcolare quei numeri. In un certo senso, sono la "materia oscura" della matematica. Sappiamo che ci sono e che costituiscono la maggioranza indescrivibile dei numeri, ma non abbiamo modo di raggiungerli. Nota: la costante di Chaitin è un esempio di numero non computabile, ma sfortunatamente ... non è calcolabile.
I diversi tipi di infinito
 Fonte: math.brown.edu, Immagine: https://pixabay.com (dominio pubblico)
Fonte: math.brown.edu, Immagine: https://pixabay.com (dominio pubblico) Sebbene gli interi siano infiniti, ci sono infinitamente più numeri reali che interi. Come può essere se gli interi sono già infiniti? È perché esistono due tipi di infinito ... numerabili e non numerabili. I numeri interi sono infinitamente numerabili, mentre i numeri reali non lo sono (perché includono anche i numeri irrazionali). Quindi questo porta a conclusioni pazze. Il numero di numeri interi positivi (0, 1, 2, ...) è esattamente uguale al numero di numeri interi positivi e negativi combinati (..., -3, -2, -1, 0, 1, 2, 3, ...). Sebbene questi due insiemi infiniti siano uguali, sono entrambi più piccoli dell'insieme infinito di numeri reali. In effetti, ci sono infinitamente più numeri tra solo due numeri interi casuali (0 e 1 per esempio) di quanti ce ne siano nell'intero insieme infinito di numeri interi!
I numeri normali
 Fonte: mathworld.wolfram.com
Fonte: mathworld.wolfram.com Un numero normale è fondamentalmente un numero irrazionale che non ha più una data cifra di un'altra. Quindi, ad esempio, nel numero 4.56856948576434 ... ogni singola cifra dovrebbe apparire all'incirca un numero uguale di volte fino ad arrivare all'infinito. Sebbene ci sia una prova approssimativa per dimostrare che la maggior parte dei numeri reali sono normali, e sospettiamo che numeri come pi ed e siano normali, non siamo ancora stati in grado di mostrarlo.
I numeri trascendentali
 Fonte: mathworld.wolfram.com
Fonte: mathworld.wolfram.com Sebbene quasi ogni singolo numero reale e complesso sia trascendentale (al contrario di algebrico, che in pratica è qualsiasi numero che sia la radice di un polinomio), ne sono noti solo pochi, principalmente perché è davvero difficile dimostrare che un numero è trascendentale. I numeri trascendentali più noti sono e e pi.
Il primo solitario
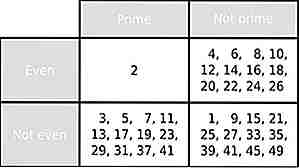 Fonte: mathworld.wolfram.com, immagine: https://commons.wikimedia.org (dominio pubblico)
Fonte: mathworld.wolfram.com, immagine: https://commons.wikimedia.org (dominio pubblico) Ogni singolo numero primo fino all'infinito è strano. Tranne 2.
L'effetto dell'infinito sulla probabilità
 Immagine: https://pixabay.com (dominio pubblico)
Immagine: https://pixabay.com (dominio pubblico) Il concetto di infinito ha alcuni effetti pazzi sulla probabilità. Se dovessi selezionare casualmente un numero reale, la probabilità che esso sia razionale (1, 2, ¾, 78/56, ...) è 0. Questo risale al fatto che i numeri irrazionali sono infinitamente infiniti, mentre i numeri razionali sono numerabilmente infiniti. E l'infinito numerabile rispetto all'infinito non numerabile è 0.
.999 ... = 1
 Immagine: https://commons.wikimedia.org (dominio pubblico)
Immagine: https://commons.wikimedia.org (dominio pubblico) .999 ... è uguale a 1. A questo punto la tua mente è probabilmente così sconvolta dal concetto di infinito che probabilmente accetterete semplicemente qualunque cosa vi diciamo, ma lo dimostreremo. Sai che .333 ... è uguale a ⅓ e .666 ... è uguale a ⅔. ⅓ + ⅔ = 1 e .333 ... + .666 ... = .999 .... Un altro modo di pensare a questo è che se .999 ... non è uguale a 1, ci dovrebbe essere un numero compreso tra .999 ... e 1. Che, grazie al concetto di infinito, non c'è.
La funzione Dirichlet
 Fonte: mathworld.wolfram.com
Fonte: mathworld.wolfram.com Secondo la funzione di Dirichlet, tra due numeri irrazionali c'è un numero razionale. La parte pazza? Ci sono numeri infinitamente più irrazionali dei numeri razionali (come abbiamo stabilito in precedenza). Quindi ... come potrebbero ogni due numeri irrazionali avere un numero razionale tra loro? Ti aspetteresti di rimanere senza numeri razionali. Ma l'infinito semplicemente non si comporta come ci aspettiamo.
L'identità di Eulero
 Fonte: mathworld.wolfram.com
Fonte: mathworld.wolfram.com L'identità di Eulero è spesso citata come esempio di bellezza matematica. È e ^ (pi * i) + 1 = 0. Contiene 5 delle costanti matematiche più fondamentali 0, 1, e, pi e i. Inoltre, tre delle operazioni aritmetiche di base avvengono esattamente una volta: addizione, moltiplicazione ed esponenziazione. Benjamin Peirce, un noto matematico disse una volta dopo averlo provato in una conferenza, "l'identità è assolutamente paradossale; non possiamo capirlo, e non sappiamo cosa significhi, ma lo abbiamo dimostrato, e quindi sappiamo che deve essere la verità. "
Il problema di Monty Hall
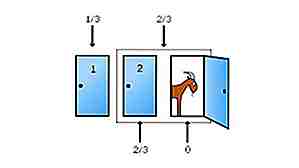 Fonte: mathworld.wolfram.com, immagine: https://commons.wikimedia.org (dominio pubblico)
Fonte: mathworld.wolfram.com, immagine: https://commons.wikimedia.org (dominio pubblico) Il problema di Monty Hall è un famoso esempio di come la probabilità può essere contro-intuitiva. Diciamo che in uno show di gioco ci sono tre porte. Dietro uno di loro c'è un'auto mentre gli altri due nascondono capre. Scegli di aprire la porta 1. L'host, tuttavia, sa cosa c'è dietro le porte. Apre la porta 3 per rivelare una capra. Ora ti chiede se vuoi cambiare la tua scelta sulla porta 2. Che cosa fai? La risposta è che dovresti cambiare la tua scelta. Perché? Perché passando alla porta 2 hai la possibilità of di vincere la macchina mentre sei sulla porta 1 hai una probabilità ⅓ all'incirca. Il modo migliore per visualizzare questa soluzione contro-intuitiva è aumentare il numero di porte. Diciamo ora che ci sono 100 porte. Scegli la porta 37. L'host ora apre tutte le porte per rivelare le capre ad eccezione della porta 83. Vuoi cambiare la tua scelta dalla 37 alla 83? O resteresti al 37? Il fatto è che le tue possibilità di vincere l'auto aumenteranno significativamente passando alla porta 83.
La differenza tra 1 milione e 1 miliardo

Un milione di secondi è di circa 11 giorni e mezzo. Un miliardo di secondi è poco meno di 32 anni.
Il principio di Pigeonhole
 Fonte: mathworld.wolfram.com, immagine: https://commons.wikimedia.org (dominio pubblico)
Fonte: mathworld.wolfram.com, immagine: https://commons.wikimedia.org (dominio pubblico) Se hai 2 tipi di calzini nel tuo cassetto e ne prendi 3 in modo casuale senza guardare, hai la garanzia di avere una coppia corrispondente. Mentre per alcune persone questo è ovvio, per altri può essere più difficile da capire. È basato su qualcosa chiamato il principio del piccione. Fondamentalmente, se hai n tipi di qualcosa, allora devi scegliere casualmente n + 1 di quella cosa per ottenere una corrispondenza. Quindi, se hai 5 tipi diversi di calzini nel tuo cassetto e ne prendi a caso 6, ti garantiamo una corrispondenza. Questo può essere bello per vestirsi al buio!
La somma di tutti i numeri interi positivi da 1 a infinito
 Fonte: vedi sotto, Immagine: https://commons.wikimedia.org (dominio pubblico)
Fonte: vedi sotto, Immagine: https://commons.wikimedia.org (dominio pubblico) Ora, preparati per possibilmente la cosa più sconvolgente che tu abbia mai sentito in tutta la tua vita. Se sommi tutti i numeri interi positivi da 1 a infinito ... cosa ottieni? Hai indovinato -1 / 12? Perché questa è la risposta giusta. Sappiamo. Questo suona assolutamente ridicolo e in una certa misura lo è. Perché? Perché aggiungere qualsiasi cosa fino all'infinito è impossibile e garantire risultati ridicoli. Per rendere le cose ancora più folli per te, questo risultato è in realtà molto ben noto in fisica, in particolare la teoria delle stringhe. Infatti, se ancora non riesci a crederci, ti suggeriamo di guardare questo video dai fisici Tony Padilla e Ed Copeland dell'Università di Nottingham. Spiegano la follia meglio di quanto possiamo - https://www.youtube.com/watch?v=w-I6XTVZXww.
Nota: il risultato deriva in gran parte dal fatto che l'infinito sfida le nostre aspettative. L'infinito non è un numero, è un concetto. Cose come addizione e sottrazione non funzionano allo stesso modo quando coinvolgi l'infinito (un po 'come la fisica non funziona allo stesso modo quando ti trovi nel mezzo di un buco nero).
Ulteriori informazioni: vale anche la pena di esaminare la somma di Ramanujan e la serie di Grandi:
https://en.wikipedia.org/wiki/Ramanujan_summation
https://en.wikipedia.org/wiki/Grandi's_series
Un'altra risorsa:
http://www.bradyharanblog.com/blog/2015/1/11/this-blog-probably-wont-help
Foto: Immagine in primo piano: https://commons.wikimedia.org (dominio pubblico), 20. max pixel, 16. Tttrung, Klein bottle2, CC BY-SA 4.0, 11. Mehran Moghtadaei, PP 1280 × 1024, CC BY- SA 3.0, 10. Stephen J. Brooks (parla), Algebraicszoom, CC BY 3.0, 6. Judy Breck via flickr, CC BY-SA 2.0, 5. Quinn Dombrowski di Chicago, USA, Euler's Identity Graffito, CC BY-SA 2.0, 3. Cmglee, Visualizzazione 1 miliardo, CC BY-SA 3.0,




