25 semplici trucchi matematici mentali che ti faranno perdere la testa

Per vedere se un numero è divisibile per tre, sommare le cifre. Se la somma è divisibile per tre, lo è anche il numero. Nota: questo funziona anche per 9.

x% di y è uguale a y% di x. Ciò significa che se il 2% di 50 è troppo difficile da capire, puoi semplicemente capovolgerlo - il 50% di 2. Molto più semplice.

Per moltiplicare un numero di 2 cifre per 11 basta aggiungere le cifre e incollare la risposta tra loro. Ad esempio 42 * 11 sarebbe 4 + 2 = 6. Ora metti il ​​6 tra il 4 e il 2 per ottenere 462.

Nota: non dimenticare di portare il 1. Per dare un altro esempio, 58 * 11 sarebbe 5 + 8 = 13. Tuttavia non puoi semplicemente mettere il 13 tra il 5 e l'8. Ciò darebbe 5138, che è ovviamente sbagliato. Devi portare quello aggiungendolo al 5. Quindi sarebbe 638.

Se è necessario moltiplicare un numero per 5, potrebbe essere più semplice farlo a metà e moltiplicarlo per 10. Ad esempio, 315 * 5 sarebbe 315/2 = 157, 5 Ora basta spostare il decimale sopra per moltiplicare per 10 e ottenere 1575.

Per approssimare una radice quadrata, fai quanto segue. Trova il prossimo quadrato perfetto inferiore. Aggiungilo al tuo numero Ora dividi per la radice quadrata del quadrato perfetto inferiore. E ora dividiamo di nuovo per 2. Sembra difficile? Ecco un esempio. Prendi 31. Il prossimo quadrato perfetto più basso è 25. Quindi 31 più 25 è 56. Ora dividi per la radice quadrata di 25. Quindi 56/5 = 11.2 Ora dividi per 2 per ottenere 5.6

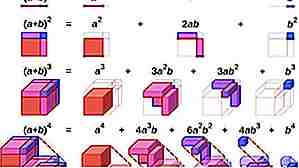
Utilizza il teorema binomiale (a + b) ^ 2 = a ^ 2 + 2ab + b ^ 2 ai numeri quadrati. Ad esempio 55 ^ 2 potrebbe essere (50 + 5) ^ 2. Ciò significa che 50 * 50 + 50 * 5 * 2 + 5 * 5 = 2500 + 500 + 25 = 3025.

Per vedere se un numero è divisibile per 8, controlla le ultime tre cifre. Se sono divisibili per 8, il numero è divisibile per 8. Ad esempio, 3423024 sarebbe divisibile per 8 perché 024/8 = 3

Per calcolare un suggerimento basta spostare il decimale di un posto a sinistra per ottenere il 10%. Quindi aggiungi metà di ciò che ti rimane per ottenere il 15% o raddoppiarlo per il 20%. Ad esempio, se il conto è $ 43, 21, $ 4, 32 è del 10%. La metà di $ 4, 32 è $ 2, 16 quindi se si desidera il 15% è sufficiente aggiungerlo. Ti dare $ 4, 32 + $ 2, 16 = $ 6, 48. Ottenere il 20% è ancora più semplice perché lo raddoppi. $ 4, 32 * 2 = $ 8, 64. Quindi, se ti senti generoso, $ 8, 64 costituirebbe un suggerimento del 20%.

Per calcolare il tuo stipendio annuale, prendi il tuo salario orario, raddoppialo e aggiungi 3 zeri. Diciamo che stai facendo $ 8 all'ora. Basta raddoppiare quello per $ 16 e quindi aggiungere tre zeri per $ 16.000.

Per approssimare le conversioni tra Celsius e Fahrenheit basta moltiplicare per 2 e aggiungere 30 (passando da C a F). Fai il contrario per andare da F a C (sottrai 30 e dividi per 2).

Per vedere se un numero è divisibile per 4 basta guardare le ultime due cifre. Se sono divisibili per 4, allora l'intero numero è divisibile per 4. Quindi 23746316 sarebbe divisibile per 4 perché 16 è divisibile per 4.

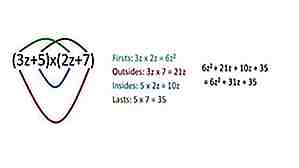
Per moltiplicare due numeri, usa il metodo FOIL (primo, esterno, interno, ultimo). Ad esempio, 25 * 37 sarebbe (20) (30) + (5) (30) + (7) (20) + (5) (7) = 925.

Nota: questo è esattamente ciò che fai quando si moltiplica su carta, è solo più facile visualizzare il metodo FOIL nella tua testa.

Per calcolare la percentuale di un numero (che non è il 10%) trova prima l'1% e poi lo moltiplica. Quindi, ad esempio, il 3% di 528 sarebbe 528 * .01 = 5, 28 (sposta il decimale di due posizioni a sinistra). Ora basta moltiplicare per 3 per ottenere 15, 84

Questo funziona particolarmente bene se uno dei numeri è già bello e rotondo (finisce in 0). Basta arrotondare l'altro numero, moltiplicare e regolare il risultato di conseguenza. Ad esempio, se vuoi calcolare 18 * 30 non hai bisogno del metodo FOIL che abbiamo fatto prima (perché 30 è già bello e rotondo). Basta fare 20 * 30 che è 600 e quindi sottrarre due 30 per 540.

Per verificare se un numero è divisibile per 6 è necessario combinare due regole di divisibilità (due e tre). Se è divisibile per 2 e 3, allora è divisibile per 6. Abbiamo già fatto divisibilità per 3 ma nel caso in cui ... anche i numeri sono divisibili per 2.

La rappresentazione decimale degli undicesimi può essere fatta moltiplicando il numeratore per 9 e ripetendolo semplicemente. Ad esempio, 1/11 = .09090909 .... e 2/11 = .18181818 ... ecc

Per quadrare qualsiasi numero a due cifre che termina con 5, basta mettere 25 alla fine e moltiplicare il primo numero con la seguente cifra. Quindi, ad esempio, 45 ^ 2 sarebbe 2025 perché 5 è la cifra successiva sopra 4 quindi 4 * 5 = 20. Ora basta mettere un 25 alla fine per il 2025.

Le rappresentazioni decimali per i nono sono solo ripetute dal numeratore. Ad esempio 1/9 = .1111111 ... e 2/9 = .2222222 ... Questa è anche una delle dimostrazioni utilizzate per mostrare che .999999 ... = 1. (dal 9/9 = .99999 ...)

Per i numeri di quadratura, un trucco possibile è aggiungere / sottrarre dal numero fino a ottenere due numeri che è possibile moltiplicare facilmente. Quindi aggiungi la differenza del numero che hai aggiunto / sottratto. Per fare un esempio, 46 ​​^ 2 potrebbe essere 42 * 50 perché 46 - 4 = 42 e 46 + 4 = 50. Quindi 42 * 50 sarebbe 2100. Ora piazza il numero che hai aggiunto / sottratto in modo da 4 ^ 2 = 16. Ora aggiungi 16 per ottenere 2116.

72 diviso per il tasso di interesse ti darà una stima approssimativa di quanti anni ci vorrebbe per raddoppiare i tuoi soldi (regola del 72).

Per fare l'aggiunta mentale, è molto più facile lavorare da sinistra a destra piuttosto che come si fa sulla carta (da destra a sinistra). Questo perché il tuo cervello riconosce e ricorda naturalmente i numeri che iniziano a sinistra. Ad esempio, per fare 376 + 581, aggiungi 300 + 500 per ottenere 800. Ora aggiungi 70 + 80, che è 150. Questo porta il totale a 950. Quindi aggiungi il 7 per ottenere 957. Fondamentalmente, rompere l'aggiunta verso il basso in parti più piccole da sinistra a destra. Un altro vantaggio di questo è che ti troverai gradualmente a casa nella soluzione. Quindi, se vuoi solo un'approssimazione, non devi aspettare che tu finisca il problema per capire quale ordine di grandezza stai lavorando (centinaia, migliaia, ecc.)

Per la sottrazione mentale, l'idea è simile all'addizione. Lavora da sinistra a destra, ma c'è un trucco in più di cui devi essere consapevole (suggerimento: si tratta di arrotondare). Diciamo che vuoi fare 632 - 487. In primo luogo, aggiungi 3 per arrotondare 487 fino al 10 più vicino, quindi 490. Ora il problema diventa 632 - 490. Questo è molto più facile. 632 - 400 è 232. Ora sottraendo 90 ottieni 142 (è 10 in più rispetto a sottrarre 100). Da lì, ricorda di aggiungere nuovamente i 3 dall'inizio. Questo ti dà 145.

Un altro trucco per moltiplicare i numeri che sono facilmente arrotondati (di solito terminano in 8 o 9), è quello di utilizzare il metodo di sottrazione. Per fare ciò, arrotondi il numero e poi sottrai. Ad esempio, 49 * 16 sarebbe 50 * 16. Questo è molto più facile da risolvere. Poiché 100 * 16 è 1600, puoi ottenerne la metà per ottenerne 800. Ora ricorda solo di sottrarre ciò che inizialmente hai arrotondato. Quindi, dal momento che hai arrotondato 49 fino a 50, era 1 * 16, che è ciò che devi sottrarre. Ciò dà 800 - 16 che è 784.

Ricorda che puoi fare tutto ciò che vuoi in un'equazione fintanto che lo fai su entrambi i lati. Inoltre, puoi fare tutto ciò che vuoi con un termine, a patto di moltiplicarlo per uno. Tieni presente che 1 ha forme infinite (2/2, (x-4) / (x-4), ecc.).

Per convertire miglia in chilometri, puoi ottenere una stima molto vicina aggiungendo il 60%. Il modo più veloce per farlo è aggiungere il 50% e quindi il 10%. Per esempio. 60 miglia in km sarebbero le seguenti: 60 * .5 = 30 e 60 * .1 = 6. Ora, 30 + 6 = 36. Aggiungi questo a 60 per ottenere 96 km. Per andare da chilometri a miglia, basta sottrarre il 40%. Puoi farlo sottraendo il 50% e aggiungendo il 10%. Quindi per ottenere 350 km in miglia sottrarre la metà di 350. Questo ti dà 175. Ora aggiungi il 10% di 350 che è 35. Questo ti lascia con 210. Nota: tieni presente che si tratta di stime molto approssimative. Più grandi saranno i tuoi numeri, più errori ci saranno.